

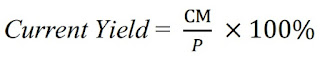
By using this method, there are still any differences of calculation result, but it’s not significant. There is only approximation of 4 digits in decimals for the result. This method gives the same result if it is compared with several methods mentioned above for the same case. In this method, the numerical case must be transferred into the NPV equation or obligation equation, and be created to the polynomial equation in term of f(x) until the error is minimum. As we know there are several methods to solve the calculation about IRR ,such as Interpolation Method by using the financial table and Trial and Error Method by using IRR Function in Excel Software but the most popular is Newton Raphson Method. This paper will present the application of numerical mathematic and discuss the alternative method to calculate and solve the problem about the value of Internal Rate Return (IRR) and desired returned rate by obligation investor. Internal Rate Return, interpolation method numerical mathematic, Newton Raphson Method, NPV equation, polynomial equation, interaction, obligation, approximation Abstrak This is too low, but you now know that the precise yield to maturity is somewhere between 6 and 7 percent or between 3 and 3.5 percent on a semi-annual basis.Fakultas Teknik Universitas Trunojoyo Madura.Plug it into the formula, and you get a P of $95. Talk the annual interest rate up by one more point to 7 percent (or 3.5 percent on a semi-annual basis).This is too high, since the purchase price is $95.92.Plug half of that (3 percent, because payments are semi-annual) it into the formula, and you get a P of $95. In the above example, begin by taking the annual interest rate up by one point to 6 percent.That means you'll effectively want to divide the annual interest rate by 2. Remember, though, you're plugging in an estimated i for semi-annual payments.

Since we know that the coupon rate is 5 percent, we can start by plugging numbers that are higher than that into the formula above to solve for P.

Since this bond is priced at a discount, we know that the yield to maturity will be higher than the coupon rate. You don’t have to make random guesses about what the interest rate might be. Now, you have to solve for i using trial and error, plugging in different values for i until you get the correct price.Įstimate the interest rate by considering the relationship between the bond price and the yield.Once you have that information, plug it into the formula P = C ∗ ( ( 1 − ( 1 / ( 1 + i ) n ) ) / i ) + M / ( ( 1 + i ) n ). Also, you need to know the amount of each coupon payment you will receive and the number of coupon payments until maturity. You need to know the face value of the bond and the present value, or purchase price. Gather the information and plug it into the formula.


 0 kommentar(er)
0 kommentar(er)
